Minesweeper
Time Limit: 1 sec
The Problem
Minesweeper is a popular and interesting computer game. Although you may know the game but also I want to give some information to you about minesweeper game. In this game at first we will get a (N*N) grid board. In this board some cell contains mines, some cell contains numbers and other cell will remain empty. In this grid some mines are randomly hidden in this grid. Suppose, in a cell a number 4 will indicate that there are 4 mines hidden in any of its adjacent 4 cells within 8 cells. In a grid left, right, up, down and diagonal cell of cell is the adjacent cell of the current cell. In the picture below 8 green cells is adjacent cell of the white cell.

Here I show you an (9*9) minesweeper board in below, before solved and after solve
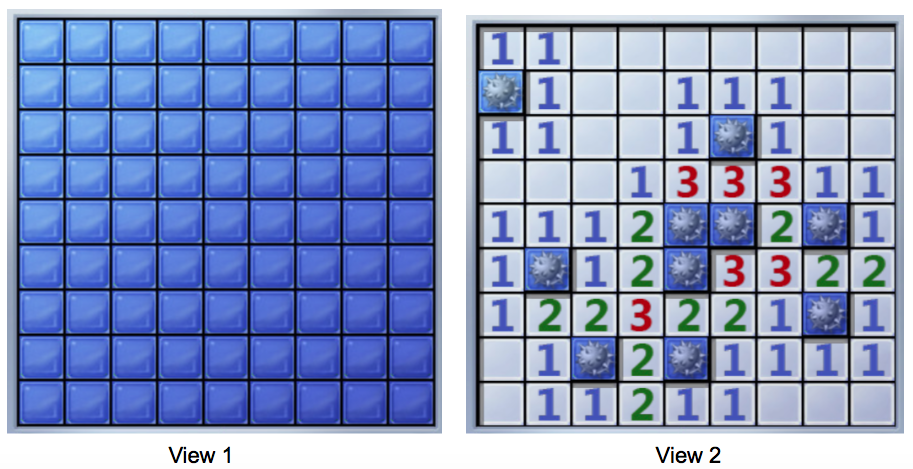
Now look at the view 1 before play this game, can you seen anything? Yes an 81 (9*9) cell board and it are totally covered by blue shed. Now look at view 2 after solved, there are 10 cells with mines, 48 cells with numbers and 23 cells are empty.
In this problem I will give you a (N*N) board with mines. You have to calculate the number of empty cell and the number of cell which contain numeric number.
The Input
The first line of the input is start with an integer T (T<=10), the number of test case. Each test case is begins with an integer N (N<=25). The next N line of input will be the grid itself, where each line will contain a string with length N. this string will only contains # (Has) as a mine and 0 (ZERO) as a covered cell.
The Output
For each input set print a single line, in each line print two integers P and Q separated by a single space. Here P is the number of cell which contains numeric number and Q is the number of empty cell.
Sample Input
2
6
00#000
0000#0
000000
0#00#0
000#00
#00000
3
0##
000
#00
Sample Output
27 3
5 1
Derivation of case 2:
When we placed numeric value in a cell counting mines to its adjacent cell then the grid will look like below.
1##
232
#10
Here 5 numeric values in 5 cells and 1 empty cell and it’s remain zero
[University Level]
ISCPC 2017 Preliminary
Problem Setter: Milton Deb